Вычисление угла на Z80: Делаем невозможное на 3.5 МГц
Привет, друзья! (Или просто читатели, кому интересно заглянуть под капот старых добрых ретро-игр). Как часто мы вспоминаем то самое волшебное время, когда каждый килобайт, каждый такт процессора Z80 на нашем любимом Спекки были на счету? Мы выжимали максимум из этих 3.5 МГц, чтобы на экране происходила магия – двигались спрайты, взрывались бомбы, бегали враги…
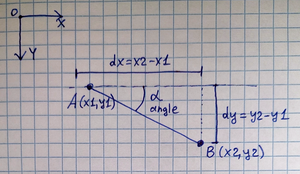
А что нужно, чтобы всё это двигалось не просто так, а умно? Например, чтобы пуля летела точно в цель? Или враг шел к игроку по самому короткому пути? Правильно – нужно знать направление. А направление – это, по сути, угол!
Но вот незадача! Наш старый добрый Z80 – это процессор целочисленный. Никаких тебе модных сопроцессоров, никаких нативных операций с плавающей точкой, синусов, косинусов или, страшно сказать, арктангенсов! Посчитать угол между двумя точками (ну, или вектором (dx, dy) – разницей координат) – это для него задачка не из простых. Это не LD A,B или ADD HL,DE. Это что-то из высшей математики, которую, казалось бы, на 3.5 МГц не осилить без тормозов.
Именно поэтому в старых играх часто использовались хитрые трюки, обходы и упрощения. Ведь каждая лишняя миллисекунда на вычисления – это проседание фреймрейта, менее отзывчивое управление, или просто игра становится скучной, потому что враги тупят и не могут тебя толком найти.
Но что, если я скажу вам, что можно получить достаточно точное значение угла для игровых целей, используя только целочисленную арифметику и небольшие таблицы? Без тормозов и с изяществом, достойным настоящего мастера ассемблера! Именно об этом мы сегодня и поговорим. Разберем самые простые (и грубые) подходы, намекнем на сложности более прямых, а потом я покажу, как можно применить немного математики (но не пугайтесь, совсем чуть-чуть!) и таблиц, чтобы заставить наш Z80 считать углы быстро и эффективно.
Готовьтесь погрузиться в мир целочисленной магии!
Быстро, но грубо… или прямо, но медленно?
Когда нужно найти угол вектора (dx, dy) на Z80, первая мысль – "как-то попроще". Самое простое – это посмотреть на знаки dx и dy и определить, в какой четверти (квадранте) находится угол. Положительные dx и dy? Значит, вниз-вправо (для Спекковских координат). Отрицательные dx и положительные dy? Вниз-влево. Это моментально, но дает точность в диапазоне 90 градусов, то есть +/- 45 градусов. Для многих задач этого недостаточно. Можно уточнить, сравнив абсолютные значения dx и dy – это даст уже 8 направлений (по 45 градусов). Быстро, но все еще грубо – как пытаться прицелиться, глядя в очень мутный бинокль.
А что насчет "прямого" подхода – угол = atan(dy / dx)? Нужен арктангенс! На PC взял функцию atan2(x, y), и готово. На Спекки? Можно сделать таблицу atan и взять из нее значение по индексу dy/dx. Но тут две проблемки:
- Деление
dy/dxна Z80 – это медленно. Наш процессор не умеет делить "из коробки", нужна подпрограмма, а это десятки или сотни тактов. Мы хотели скорости, а получили тормоза. - Как использовать
dy/dxкак индекс для таблицы? Отношениеdy/dxможет быть от нуля до бесконечности! Табличка на 256 байт никак не покроет весь этот диапазон с нужной точностью. Даже если схитрить и считать угол только в пределах 0-45 градусов (где0 <= dy/dx <= 1), все равно нужно как-то масштабировать это отношение, а для этого опять нужно деление или сложное умножение.
Так что прямой табличный atan(y/x) на Z80 – это не самое изящное и не самое быстрое решение. Нужно обойти эту проблему с делением!
Наш трюк: логарифмы и две таблицы
А вот и наша хитрость! Вместо того чтобы считать dy/dx (где деление), давайте вспомним свойство логарифмов: log2(Y / X) = log2(Y) - log2(X). Деление превратилось в вычитание! А вычитание Z80 делает моментально. Бинго!
Идея такая:
-
У нас есть
dxиdy. Сначала мы их "нормализуем": делаем положительными (берем абсолютное значение) и, если нужно, меняем местами, чтобы одна координата (назовем ее X) всегда была больше или равна другой (назовем ее Y). Это нужно, чтобы работать только с углами от 0 до 45 градусов и чтобы разность логарифмов была удобной. Запоминаем, какие трансформации мы сделали (знаки и был ли своп). -
Теперь у нас есть положительные
XиY, гдеX >= Y. Нам нужно найтиlog2(X)иlog2(Y). А для этого у нас есть первая таблица:log2tab. Она хранитlog2(число)для каждого числа от 0 до 255, но не просто так, а умноженное на скейл (например, 32), чтобы сохранить точность. Просто беремlog2tab[X]иlog2tab[Y]. -
Вычисляем разность:
разность_логарифмов = log2tab[X]–log2tab[Y]. Это быстрое вычитание! -
Эта "разность логарифмов" связана с отношением
X/Y. Чем меньше разность, тем ближе X и Y (угол к 45 градусам). Чем больше разность, тем меньше Y по сравнению с X (угол ближе к 0). Нам нужна таблица, которая по этой разности логарифмов скажет нам, какой угол между 0 и 45 градусами этому соответствует. Это наша вторая таблица:atan2pow_tab. Она хранит значения угла (масштабированные) по индексу, равному разности логарифмов.
Итого: Две маленькие таблицы (по 256 байт каждая), два обращения к первой таблице, одно быстрое вычитание, одно обращение ко второй таблице – и мы получаем "базовый" угол в диапазоне 0-45 градусов! Никакого медленного деления!
Собираем всё вместе: алгоритм на пальцах
Вот как это выглядит целиком, шаг за шагом:
-
Вход: Получаем
dxиdy. -
Особые случаи: Проверяем, если
dx=0иdy=0(нулевой вектор, нет угла) или если один из них ноль (угол 0, 90, 180, 270). Возвращаем соответствующее значение быстро. -
Нормализация: Берем абсолютные значения
x = abs(dx),y = abs(dy). Запоминаем знакиdxиdy(например, в битах регистра). Сравниваемxиy. Еслиx < y, меняем их местами (x = y_original,y = x_original) и запоминаем, что поменяли (флаг "mirror"). Теперь у нас гарантированноx >= y > 0, то есть оба не равны нулю (кроме основых случаев, которые мы обработали). -
Разность логарифмов: Идем в
log2tabпо индексуx, получаемlogX_scaled. Идем вlog2tabпо индексуy, получаемlogY_scaled. Вычисляемk_scaled = logX_scaled - logY_scaled. -
Базовый угол: Используем
k_scaledкак индекс дляatan2pow_tab. Берем значениеang_0_45_scaled(число 0-255, представляющее 0-45 градусов). -
Масштабирование: Масштабируем
ang_0_45_scaledдо 16-битного значения (0-65535), которое покрывает 360 градусов. Просто сдвигаем его влево на 5 бит (<< 5). Получается число, представляющее угол в 0-45 градусах, но уже в 16-битном масштабе. -
Финальная сборка: Используем сохраненные флаги (знаки
dx,dyиmirror), чтобы "отразить" этот 16-битный угол в нужный квадрант. Если был "mirror" – вычитаем из 90 градусов (в 16-битном масштабе). Еслиdxбыл отрицательный – вычитаем из 180. Еслиdyбыл отрицательный – вычитаем из 360. Это делается простыми 16-битными вычитаниями.
И вот наш результат – 16-битное число, точно представляющее угол вектора (dx, dy)!
Вот как выглядят генераторы таблиц на JS (просто чтобы было понятно, что в них лежит) и примерная реализация на ассемблере Z80:
// JS код для генерации таблиц
const log2tab = new Uint8Array(256);
const atan2pow_tab = new Uint8Array(256);
function prepareTables() {
// log2
let i = 0;
for (i = 0; i < 256; i ++) {
log2tab[i] = (i > 0) ? Math.floor(Math.log2(i) * 32) : 0;
}
// atan(2^k)
for (i = 0; i < 256; i ++) {
atan2pow_tab[i] = (i > 0) ? Math.floor(Math.atan(Math.pow(2, - i / 32)) * 256 / (Math.PI / 4)) : 255;
}
}
prepareTables(); // Генерируем таблицы
// Теперь log2tab и atan2pow_tab можно скопировать в ассемблерный код как байтовые данные
А вот и код на Javascript для вычисления угла нашим методом.
function logAngle(x, y) {
// Получаем "чистые" значения x, y в диапазоне от 0 до 45 градусов
if (x === 0 && y === 0) {
// Частный случай для нулевого отрезка
return 0;
}
let is_x_neg = 0;
if (x < 0) {
is_x_neg = 1;
x = 0 - x;
}
let is_y_neg = 0;
if (y < 0) {
is_y_neg = 1;
y = 0 - y;
}
let is_mirr = 0;
if (x < y) {
// Exchange x and y
is_mirr = 1;
let t = x;
x = y;
y = t;
}
// Now X and Y equals to angle from 0 to 45
let ang = 0;
if (y == 0) {
// Частный случай - суб-угол 0 градусов
} else {
// Считаем угол по упрощённой формуле atan(2^k), где k = log2(x) - log2(y)
ang = atan2pow_tab[log2tab[x] - log2tab[y]];
}
// Полученное значение помещаем в нужный квадрант
// Чтобы сохранить точность, сдвигаем значение влево на 5 бит и тем самым расширяем до 16 бит
let ang16 = (ang << 5);
if (is_mirr) {
ang16 = 0x4000 - ang16;
}
if (is_x_neg) {
ang16 = 0x8000 - ang16;
}
if (is_y_neg) {
ang16 = 0x10000 - ang16;
}
//ang16 = ang16 & 0xff00; // Если нужна 8-битная точность
return ang16 * 360 / 65536; // Если нужно значение в диапазоне от 0 до 360
}
Ну и, наконец, фанфары! Наш финальный код на Z80 Assembler, который делает то же самое, что и код на Javascript выше, но заточен под наш любимый Спекки.
; Calculate 11-bit angle value (aligned to 16 bit)
; Input: HL = (Y1, X1), DE = (Y2, X2) - Start and end points of the vector, [0, 0xff], non-signed values.
; Output: HL = angle value from 0 to 0xffff (0 = 0 degrees, 0xffff = 359.9 degrees), only the most 11 bits have value
math_angle8x8
ld c, 0 ; Keep flags here. C.0 = is_x_neg, C.1 = is_y_neg, C.2 = is_mirror
ld a, e
sub l ; A = dx
jr nc, .a1 ; dx >= 0
; dx < 0
set 0, c ; is_x_neg = 1
ld e, a
xor a
sub e ; dx = 0 - dx
.a1 ld e, a
; check dy
ld a, d
sub h
jr nc, .a2
; dy < 0
set 1, c
ld d, a
xor a
sub d
.a2 ld d, a
or e ; A = dx | dy
jr z, .a3 ; dx = 0, dy = 0, special condition
ld a, e
cp d
jr nc, .a5 ; dx >= dy
; dx < dy, we need mirroring
; A = E here
set 2, c
ld e, d
ld d, a
; D and E was exchanged
.a5 ld a, d
or a
jr z, .a4
; All flags were set, let's calculate
ld l, e
ld h, log2tab >> 8 ; Upper byte of the table address
ld a, (hl) ; A = log2(dx)
ld l, d
sub (hl) ; A = log2(dx) - log2(dy)
ld l, a
ld h, atan2pow_tab >> 8 ; Upper byte of the table address
ld a, (hl) ; A = atan2pow_tab(log2(dx) - log2(dy))
; We got angle value from 0 to 45
; Now mirror this value back
ld l, a
ld h, 0
add hl, hl
add hl, hl
add hl, hl
add hl, hl
add hl, hl
bit 2, c
jr z, .a6
; Mirror 0..45 to 45..90 if flag was set
ld de, 0x4000
ex de, hl
sub hl, de
.a6 bit 0, c
jr z, .a7
; Mirror X
ld de, 0x8000
ex de, hl
sub hl, de
.a7 bit 1, c
jr z, .a8
; Mirror Y
ld de, 0
ex de, hl
sub hl, de
.a8 ; Result in HL
; Main return point
ret
.a3 ; Special case: dx = 0, dy = 0
ld hl, 0
ret
.a4 ; Special case: dy = 0
ld hl, 0
jr .a6 ; Let's use correct quadrant
; Those tables should be aligned by 256 bytes in RAM
align 256
log2tab
; Those values are calculated as floor(log2(i) * 32) where i = 0..255
db 0, 0, 32, 50, 64, 74, 82, 89, 96, 101, 106, 110, 114, 118, 121, 125
db 128, 130, 133, 135, 138, 140, 142, 144, 146, 148, 150, 152, 153, 155, 157, 158
db 160, 161, 162, 164, 165, 166, 167, 169, 170, 171, 172, 173, 174, 175, 176, 177
db 178, 179, 180, 181, 182, 183, 184, 185, 185, 186, 187, 188, 189, 189, 190, 191
db 192, 192, 193, 194, 194, 195, 196, 196, 197, 198, 198, 199, 199, 200, 201, 201
db 202, 202, 203, 204, 204, 205, 205, 206, 206, 207, 207, 208, 208, 209, 209, 210
db 210, 211, 211, 212, 212, 213, 213, 213, 214, 214, 215, 215, 216, 216, 217, 217
db 217, 218, 218, 219, 219, 219, 220, 220, 221, 221, 221, 222, 222, 222, 223, 223
db 224, 224, 224, 225, 225, 225, 226, 226, 226, 227, 227, 227, 228, 228, 228, 229
db 229, 229, 230, 230, 230, 231, 231, 231, 231, 232, 232, 232, 233, 233, 233, 234
db 234, 234, 234, 235, 235, 235, 236, 236, 236, 236, 237, 237, 237, 237, 238, 238
db 238, 238, 239, 239, 239, 239, 240, 240, 240, 241, 241, 241, 241, 241, 242, 242
db 242, 242, 243, 243, 243, 243, 244, 244, 244, 244, 245, 245, 245, 245, 245, 246
db 246, 246, 246, 247, 247, 247, 247, 247, 248, 248, 248, 248, 249, 249, 249, 249
db 249, 250, 250, 250, 250, 250, 251, 251, 251, 251, 251, 252, 252, 252, 252, 252
db 253, 253, 253, 253, 253, 253, 254, 254, 254, 254, 254, 255, 255, 255, 255, 255
atan2pow_tab
; Those values are calculated as floor(atan(pow(2, - i / 32)) * 256 / (PI / 4)) where i = 0..255
db 255, 252, 248, 245, 241, 238, 234, 231, 227, 224, 220, 217, 214, 210, 207, 203
db 200, 197, 194, 190, 187, 184, 181, 177, 174, 171, 168, 165, 162, 159, 156, 153
db 151, 148, 145, 142, 140, 137, 134, 132, 129, 127, 124, 122, 119, 117, 115, 113
db 110, 108, 106, 104, 102, 100, 98, 96, 94, 92, 90, 88, 86, 84, 83, 81
db 79, 78, 76, 75, 73, 71, 70, 68, 67, 66, 64, 63, 62, 60, 59, 58
db 57, 55, 54, 53, 52, 51, 50, 49, 48, 47, 46, 45, 44, 43, 42, 41
db 40, 39, 38, 38, 37, 36, 35, 34, 34, 33, 32, 32, 31, 30, 30, 29
db 28, 28, 27, 26, 26, 25, 25, 24, 24, 23, 23, 22, 22, 21, 21, 20
db 20, 19, 19, 19, 18, 18, 17, 17, 17, 16, 16, 16, 15, 15, 15, 14
db 14, 14, 13, 13, 13, 12, 12, 12, 12, 11, 11, 11, 11, 10, 10, 10
db 10, 9, 9, 9, 9, 9, 8, 8, 8, 8, 8, 8, 7, 7, 7, 7
db 7, 7, 6, 6, 6, 6, 6, 6, 6, 5, 5, 5, 5, 5, 5, 5
db 5, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 3, 3
db 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 2, 2, 2, 2, 2, 2
db 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 1, 1
db 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
Почему это круто?
В итоге, что мы получили, используя этот трюк с логарифмами и таблицами?
-
Скорость! Никаких медленных подпрограмм деления! Вся магия – это обращения к памяти и быстрые целочисленные операции. Угол считается очень быстро, не "тормозя" игру.
-
Размер! Всего 512 байт на две таблицы, плюс немного кода. Это подходит для большинства игр, даже на 48K моделях ZX.
-
Точность! Мы получаем 11-битное значение угла, что дает очень приличное разрешение (примерно 0.175 градуса на единицу). Для игровых задач этой дискретности более чем достаточно! Если не нужна такая точность, а есть желание уложиться в 8 бит (это будет примерно 1,4 градуса на единицу), то можно ещё немного упростить код.
-
Изящество! Превратить деление в вычитание с помощью логарифмов – это красивое математическое решение, идеально подходящее для ограниченного железа.
Этот алгоритм – отличный пример того, как можно решать, казалось бы, сложные задачи на Z80, используя умные математические идеи и эффективную работу с памятью. Именно такие находки и позволяли создавать на Спекки те самые, незабываемые игры!
Заключение
Вот мы и прошли этот путь – от грубых квадрантов и приблизительных оценок до получения достаточно точного значения угла с помощью таблиц логарифмов и арктангенсов от степеней двойки. Мы увидели, как задача, которая кажется невыполнимой без плавающей точки и тригонометрических функций "из коробки", решается быстро и эффективно на нашем старом добром 3.5-мегагерцовом Z80.
Этот алгоритм – всего лишь один из множества примеров того, на какие хитрости и изящные решения шли (и до сих пор идут!) разработчики для ретро-платформ. Каждая тактовая частота, каждый байт памяти имели значение. И вместо того, чтобы унывать от ограничений, люди придумывали такие вот алгоритмы, превращая кажущиеся недостатки в повод для творческого подхода.
Именно в таких задачах и их решениях проявляется вся красота и искусство разработки под ретро-железо. Это не просто кодинг, это оптимизация на грани возможного, поиск неочевидных путей и использование математических трюков, которые, возможно, давно забыты в мире гигагерц и гигабайт.
Надеюсь, эта статья была для вас не просто техническим разбором, а еще и маленьким путешествием в мир тех самых решений, которые делали игры на ZX Spectrum такими особенными. Возможно, вы увидели, как можно применить этот алгоритм в своих собственных проектах? Или, может быть, вспомнили какие-то другие хитрые способы вычисления углов или других функций на Z80?
Не стесняйтесь делиться своими мыслями, задавать вопросы или рассказывать о своих находках в комментариях под этим постом! Обмен опытом – это самое ценное в нашем небольшом, но дружном ретро-комьюнити.
Спасибо вам огромное за внимание! До новых встреч в мире ретро-программирования!
С любовью к Спекки и его волшебству,
P.S. Весь код можно скачать в нашем Git.

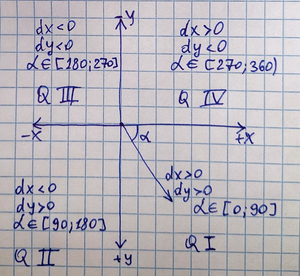


Мне кажется всегда можно обойтись вектором. Причём, не нормированным, т.е. обойтись целочисленной арифметикой. Чтобы понадобился прям угол.. ну я даже не знаю, что за задача такая.
Действительно, в чистом виде редко когда нужен именно угол. Разве что направление поворота какого-нибудь спрайта определить.
Чаще всего нужны зависимые от угла штуки, например, sin и cos угла – чтобы посчитать компоненты вектора направления.
Но иногда без него прям не обойтись. Например, если нужно протрассировать луч через игровое поле, или в алгоритме поиска кратчайшего пути по туннелю – там именно угол имеет решающее значение.