Angle Calculation on Z80: Doing the Impossible at 3.5 MHz
Hello, friends! (Or just readers interested in peeking under the hood of good old retro games). How often do we recall that magical time when every kilobyte, every Z80 clock cycle on our beloved Speccy counted? We squeezed the most out of those 3.5 MHz to make magic happen on screen – sprites moved, bombs exploded, enemies ran…
But what does it take for all of this to move not just randomly, but smartly? For instance, for a bullet to fly precisely to its target? Or for an enemy to follow the shortest path to the player? That’s right – you need to know the direction. And direction is, essentially, an angle!
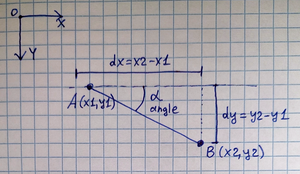
But here’s the catch! Our good old Z80 is an integer processor. No fancy co-processors, no native floating-point operations, sines, cosines, or, dare I say, arctangents! Calculating the angle between two points (or a vector (dx, dy) – the coordinate difference) is no simple task for it. It’s not LD A,B or ADD HL,DE. It’s something from higher mathematics that, it would seem, couldn’t be handled at 3.5 MHz without slowdowns.
That’s why old games often employed clever tricks, workarounds, and simplifications. Because every extra millisecond spent on calculations means a drop in framerate, less responsive controls, or simply a boring game because enemies are dumb and can’t really find you.
But what if I told you that you can get a sufficiently accurate angle value for game purposes using only integer arithmetic and small lookup tables? Without slowdowns and with an elegance worthy of a true assembly master! That’s exactly what we’ll discuss today. We’ll break down the simplest (and roughest) approaches, hint at the complexities of more direct ones, and then I’ll show you how to apply a little math (but don’t worry, just a tiny bit!) and tables to make our Z80 calculate angles quickly and efficiently.
Get ready to dive into the world of integer magic!
Fast, but Crude… or Direct, but Slow?
When you need to find the angle of a vector (dx, dy) on the Z80, the first thought is "something simpler". The simplest is to look at the signs of dx and dy and determine which quadrant the angle is in. Positive dx and dy? That means down-right (for Speccy’s coordinate system). Negative dx and positive dy? Down-left. This is instantaneous but provides accuracy within a 90-degree range, meaning +/- 45 degrees. For many tasks, this isn’t enough. You can refine it by comparing the absolute values of dx and dy – this will yield 8 directions (45 degrees each). Fast, but still crude – like trying to aim while looking through a very blurry binocular.
What about the "direct" approach – angle = atan(dy / dx)? Arctangent is needed! On a PC, you’d just use atan2(x, y), and you’re done. On the Speccy? You could create an atan table and get the value from it using dy/dx as an index. But there are two issues here:
- Division
dy/dxon the Z80 is slow. Our processor doesn’t have native division; it requires a subroutine, which takes tens or hundreds of clock cycles. We wanted speed, but got slowdowns. - How to use
dy/dxas a table index? The ratiody/dxcan range from zero to infinity! A 256-byte table won’t cover this entire range with sufficient precision. Even if you cheat and calculate the angle only within 0-45 degrees (where0 <= dy/dx <= 1), you still need to scale this ratio somehow, which again requires division or complex multiplication.
So, a direct table-based atan(y/x) on the Z80 is neither the most elegant nor the fastest solution. We need to bypass this division problem!
Our Trick: Logarithms and Two Tables
And here’s our trick! Instead of calculating dy/dx (which involves division), let’s recall a property of logarithms: log2(Y / X) = log2(Y) - log2(X). Division has turned into subtraction! And the Z80 performs subtraction instantaneously. Bingo!
The idea is this:
-
We have
dxanddy. First, we ‘normalize’ them: make them positive (take the absolute value) and, if necessary, swap them so that one coordinate (let’s call it X) is always greater than or equal to the other (let’s call it Y). This is necessary to work only with angles from 0 to 45 degrees and to make the logarithm difference convenient. We keep track of which transformations we made (signs and whether a swap occurred). -
Now we have positive
XandY, whereX >= Y. We need to findlog2(X)andlog2(Y). For this, we have our first table:log2tab. It storeslog2(number)for each number from 0 to 255, but not just the raw value; it’s scaled (e.g., by 32) to maintain precision. We simply takelog2tab[X]andlog2tab[Y]. -
Calculate the difference:
log_difference = log2tab[X]–log2tab[Y]. This is a fast subtraction! -
This "log difference" is related to the ratio
X/Y. The smaller the difference, the closer X and Y are (angle closer to 45 degrees). The larger the difference, the smaller Y is compared to X (angle closer to 0). We need a table that, based on this log difference, tells us which angle between 0 and 45 degrees corresponds to it. This is our second table:atan2pow_tab. It stores angle values (scaled) indexed by the log difference.
In summary: Two small tables (256 bytes each), two lookups in the first table, one fast subtraction, one lookup in the second table – and we get a "base" angle in the 0-45 degree range! No slow division!
Putting It All Together: Algorithm Explained
Here’s how it looks entirely, step by step:
-
Input: We get
dxanddy. -
Special Cases: Check if
dx=0anddy=0(zero vector, no angle) or if one of them is zero (angle 0, 90, 180, 270). Return the corresponding value quickly. -
Normalization: Take the absolute values
x = abs(dx),y = abs(dy). Store the signs ofdxanddy(e.g., in register bits). Comparexandy. Ifx < y, swap them (x = y_original,y = x_original) and remember that they were swapped (a ‘mirror’ flag). Now we are guaranteed to havex >= y > 0, meaning both are non-zero (except for the special cases we handled). -
Log Difference: Go to
log2tabwith indexx, getlogX_scaled. Go tolog2tabwith indexy, getlogY_scaled. Calculatek_scaled = logX_scaled - logY_scaled. -
Base Angle: Use
k_scaledas an index foratan2pow_tab. Take the valueang_0_45_scaled(a number from 0-255, representing 0-45 degrees). -
Scaling: Scale
ang_0_45_scaledto a 16-bit value (0-65535), which covers 360 degrees. Simply shift it left by 5 bits (<< 5). The result is a number representing the angle in 0-45 degrees, but now in 16-bit scale. -
Final Assembly: Use the saved flags (signs of
dx,dyandmirror) to ‘reflect’ this 16-bit angle into the correct quadrant. If ‘mirror’ was set – subtract from 90 degrees (in 16-bit scale). Ifdxwas negative – subtract from 180. Ifdywas negative – subtract from 360. This is done with simple 16-bit subtractions.
And here’s our result – a 16-bit number accurately representing the angle of the vector (dx, dy)!
Here’s how the table generators look in JS (just to illustrate what they contain) and a rough Z80 assembly implementation:
// JS code for table generation
const log2tab = new Uint8Array(256);
const atan2pow_tab = new Uint8Array(256);
function prepareTables() {
// log2
let i = 0;
for (i = 0; i < 256; i ++) {
log2tab[i] = (i > 0) ? Math.floor(Math.log2(i) * 32) : 0;
}
// atan(2^k)
for (i = 0; i < 256; i ++) {
atan2pow_tab[i] = (i > 0) ? Math.floor(Math.atan(Math.pow(2, - i / 32)) * 256 / (Math.PI / 4)) : 255;
}
}
prepareTables(); // Generate tables
// Now log2tab and atan2pow_tab can be copied into assembly code as byte data
And here’s the Javascript code for calculating the angle using our method.
function logAngle(x, y) {
// Get "clean" x, y values in the 0 to 45 degree range
if (x === 0 && y === 0) {
// Special case for zero vector
return 0;
}
let is_x_neg = 0;
if (x < 0) {
is_x_neg = 1;
x = 0 - x;
}
let is_y_neg = 0;
if (y < 0) {
is_y_neg = 1;
y = 0 - y;
}
let is_mirr = 0;
if (x < y) {
// Exchange x and y
is_mirr = 1;
let t = x;
x = y;
y = t;
}
// Now X and Y are configured for an angle from 0 to 45 degrees
let ang = 0;
if (y == 0) {
// Special case - sub-angle of 0 degrees
} else {
// Calculate the angle using the simplified formula atan(2^k), where k = log2(x) - log2(y)
ang = atan2pow_tab[log2tab[x] - log2tab[y]];
}
// Place the obtained value into the correct quadrant
// To preserve precision, shift the value left by 5 bits, thus expanding it to 16 bits
let ang16 = (ang << 5);
if (is_mirr) {
ang16 = 0x4000 - ang16;
}
if (is_x_neg) {
ang16 = 0x8000 - ang16;
}
if (is_y_neg) {
ang16 = 0x10000 - ang16;
}
//ang16 = ang16 & 0xff00; // If 8-bit precision is needed
return ang16 * 360 / 65536; // If a value in the 0 to 360 range is needed
}
And finally, fanfare! Our final Z80 Assembler code, which does the same as the Javascript code above, but tailored for our beloved Speccy.
; Calculate 11-bit angle value (aligned to 16 bit)
; Input: HL = (Y1, X1), DE = (Y2, X2) - Start and end points of the vector, [0, 0xff], unsigned values.
; Output: HL = angle value from 0 to 0xffff (0 = 0 degrees, 0xffff = 359.9 degrees), only the most significant 11 bits hold meaningful value
math_angle8x8
ld c, 0 ; Keep flags here. C.0 = is_x_neg, C.1 = is_y_neg, C.2 = is_mirror
ld a, e
sub l ; A = dx
jr nc, .a1 ; dx >= 0
; dx < 0
set 0, c ; is_x_neg = 1
ld e, a
xor a
sub e ; dx = 0 - dx
.a1 ld e, a
; check dy
ld a, d
sub h
jr nc, .a2
; dy < 0
set 1, c
ld d, a
xor a
sub d
.a2 ld d, a
or e ; A = dx | dy
jr z, .a3 ; dx = 0, dy = 0, special condition
ld a, e
cp d
jr nc, .a5 ; dx >= dy
; dx < dy, we need mirroring
; A = E here
set 2, c
ld e, d
ld d, a
; D and E were exchanged
.a5 ld a, d
or a
jr z, .a4
; All flags were set, let's calculate
ld l, e
ld h, log2tab >> 8 ; Upper byte of the table address
ld a, (hl) ; A = log2(dx)
ld l, d
sub (hl) ; A = log2(dx) - log2(dy)
ld l, a
ld h, atan2pow_tab >> 8 ; Upper byte of the table address
ld a, (hl) ; A = atan2pow_tab(log2(dx) - log2(dy))
; We got angle value from 0 to 45
; Now mirror this value back
ld l, a
ld h, 0
add hl, hl
add hl, hl
add hl, hl
add hl, hl
add hl, hl
bit 2, c
jr z, .a6
; Mirror 0..45 to 45..90 if flag was set
ld de, 0x4000
ex de, hl
sbc hl, de
.a6 bit 0, c
jr z, .a7
; Mirror X
ld de, 0x8000
ex de, hl
sbc hl, de
.a7 bit 1, c
jr z, .a8
; Mirror Y
ld de, 0
ex de, hl
sbc hl, de
.a8 ; Result in HL
; Main return point
ret
.a3 ; Special case: dx = 0, dy = 0
ld hl, 0
ret
.a4 ; Special case: dy = 0
ld hl, 0
jr .a6 ; Let's use the correct quadrant
; These tables should be aligned by 256 bytes in RAM
align 256
log2tab
; These values are calculated as floor(log2(i) * 32) where i = 0..255
db 0, 0, 32, 50, 64, 74, 82, 89, 96, 101, 106, 110, 114, 118, 121, 125
db 128, 130, 133, 135, 138, 140, 142, 144, 146, 148, 150, 152, 153, 155, 157, 158
db 160, 161, 162, 164, 165, 166, 167, 169, 170, 171, 172, 173, 174, 175, 176, 177
db 178, 179, 180, 181, 182, 183, 184, 185, 185, 186, 187, 188, 189, 189, 190, 191
db 192, 192, 193, 194, 194, 195, 196, 196, 197, 198, 198, 199, 199, 200, 201, 201
db 202, 202, 203, 204, 204, 205, 205, 206, 206, 207, 207, 208, 208, 209, 209, 210
db 210, 211, 211, 212, 212, 213, 213, 213, 214, 214, 215, 215, 216, 216, 217, 217
db 217, 218, 218, 219, 219, 219, 220, 220, 221, 221, 221, 222, 222, 222, 223, 223
db 224, 224, 224, 225, 225, 225, 226, 226, 226, 227, 227, 227, 228, 228, 228, 229
db 229, 229, 230, 230, 230, 231, 231, 231, 231, 232, 232, 232, 233, 233, 233, 234
db 234, 234, 234, 235, 235, 235, 236, 236, 236, 236, 237, 237, 237, 237, 238, 238
db 238, 238, 238, 239, 239, 239, 239, 240, 240, 240, 241, 241, 241, 241, 241, 242
db 242, 242, 242, 243, 243, 243, 243, 244, 244, 244, 244, 245, 245, 245, 245, 245
db 246, 246, 246, 246, 247, 247, 247, 247, 247, 248, 248, 248, 248, 249, 249, 249
db 249, 249, 250, 250, 250, 250, 250, 251, 251, 251, 251, 251, 252, 252, 252, 252
db 253, 253, 253, 253, 253, 253, 254, 254, 254, 254, 254, 255, 255, 255, 255, 255
atan2pow_tab
; These values are calculated as floor(atan(pow(2, - i / 32)) * 256 / (PI / 4)) where i = 0..255
db 255, 252, 248, 245, 241, 238, 234, 231, 227, 224, 220, 217, 214, 210, 207, 203
db 200, 197, 194, 190, 187, 184, 181, 177, 174, 171, 168, 165, 162, 159, 156, 153
db 151, 148, 145, 142, 140, 137, 134, 132, 129, 127, 124, 122, 119, 117, 115, 113
db 110, 108, 106, 104, 102, 100, 98, 96, 94, 92, 90, 88, 86, 84, 83, 81
db 79, 78, 76, 75, 73, 71, 70, 68, 67, 66, 64, 63, 62, 60, 59, 58
db 57, 55, 54, 53, 52, 51, 50, 49, 48, 47, 46, 45, 44, 43, 42, 41
db 40, 39, 38, 38, 37, 36, 35, 34, 34, 33, 32, 32, 31, 30, 30, 29
db 28, 28, 27, 26, 26, 25, 25, 24, 24, 23, 23, 22, 22, 21, 21, 20
db 20, 19, 19, 19, 18, 18, 17, 17, 17, 16, 16, 16, 15, 15, 15, 14
db 14, 14, 13, 13, 13, 12, 12, 12, 12, 11, 11, 11, 11, 10, 10, 10
db 10, 9, 9, 9, 9, 9, 8, 8, 8, 8, 8, 8, 7, 7, 7, 7
db 7, 7, 6, 6, 6, 6, 6, 6, 6, 5, 5, 5, 5, 5, 5, 5
db 5, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 3, 3, 3
db 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 2, 2, 2, 2, 2, 2
db 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2
db 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
Why is this cool?
So, what did we achieve by using this trick with logarithms and tables?
-
Speed! No slow division subroutines! All the magic lies in memory accesses and fast integer operations. The angle is calculated very quickly, without ‘slowing down’ the game.
-
Size! Only 512 bytes for two tables, plus a bit of code. This is suitable for most games, even on 48K ZX models.
-
Precision! We get an 11-bit angle value, which provides very decent resolution (approximately 0.175 degrees per unit). For game purposes, this granularity is more than sufficient! If such precision isn’t required, and you want to fit within 8 bits (which would be about 1.4 degrees per unit), you can simplify the code further.
-
Elegance! Transforming division into subtraction using logarithms is an elegant mathematical solution, perfectly suited for limited hardware.
This algorithm is an excellent example of how seemingly complex problems can be solved on the Z80 using clever mathematical ideas and efficient memory utilization. It’s precisely such discoveries that allowed those unforgettable games to be created on the Speccy!
Conclusion
So, we’ve journeyed through this path – from crude quadrants and rough estimations to obtaining a sufficiently accurate angle value using logarithm tables and arctangents of powers of two. We’ve seen how a task that seems impossible without floating-point and ‘out-of-the-box’ trigonometric functions can be solved quickly and efficiently on our good old 3.5 MHz Z80.
This algorithm is just one of many examples of the ingenious tricks and elegant solutions developers used (and still use!) for retro platforms. Every clock cycle, every byte of memory mattered. And instead of despairing over limitations, people devised algorithms like this, transforming perceived drawbacks into opportunities for creative approaches.
It is in such problems and their solutions that the full beauty and art of retro hardware development are revealed. It’s not just coding; it’s optimization at the edge of what’s possible, seeking non-obvious paths, and employing mathematical tricks that might be long forgotten in a world of gigahertz and gigabytes.
I hope this article was not just a technical breakdown for you, but also a small journey into the world of those very solutions that made games on the ZX Spectrum so special. Perhaps you’ve seen how this algorithm can be applied in your own projects? Or maybe you remembered other clever ways to calculate angles or other functions on the Z80?
Feel free to share your thoughts, ask questions, or tell us about your own discoveries in the comments below this post! Sharing knowledge is the most valuable thing in our small but friendly retro community.
Thank you very much for your attention! See you next time in the world of retro programming!
With love for the Speccy and its magic,
P.S. All code can be downloaded from our Git repository.

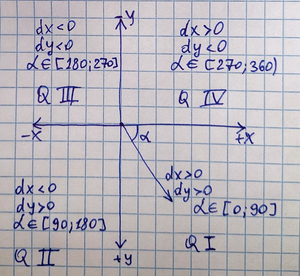


Мне кажется всегда можно обойтись вектором. Причём, не нормированным, т.е. обойтись целочисленной арифметикой. Чтобы понадобился прям угол.. ну я даже не знаю, что за задача такая.
Действительно, в чистом виде редко когда нужен именно угол. Разве что направление поворота какого-нибудь спрайта определить.
Чаще всего нужны зависимые от угла штуки, например, sin и cos угла – чтобы посчитать компоненты вектора направления.
Но иногда без него прям не обойтись. Например, если нужно протрассировать луч через игровое поле, или в алгоритме поиска кратчайшего пути по туннелю – там именно угол имеет решающее значение.